ESERCIZI SVOLTI DULLE DISEQUAZIONI INTERE DI 2° GRADO

 

Se non ricordi tutti i casi che si possono presentare vai a…

 

1.          

 

Applicando la formula risolutiva si calcolano le eventuali radici dell’ equazione associata:

 

   quindi

       e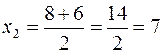    

Pertanto possiamo scrivere   .

Studiando il segno del prodotto otteniamo:

:                             :    

Quindi si ha:

                                                                                                 

                                                                                                   valori di x

                _ _ _ _ _                                                       

               _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

 

Segno del          +                  _                        +

Prodotto

 

 

Quindi possiamo concludere che le soluzioni della disequazione iniziale sono gli intervalli .

 

2.          

 

Applicando la formula risolutiva si calcolano le eventuali radici dell’ equazione associata:

 

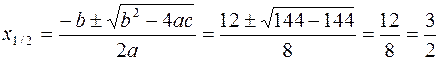
Allora possiamo scrivere     e le soluzioni della disequazione saranno: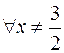

 

3.          

 

Applicando la formula risolutiva si calcolano le eventuali radici dell’ equazione associata:

 

 

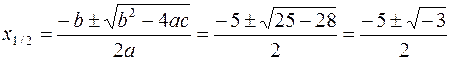
il numero – 3 è negativo pertanto la sua radice quadrata non esiste e possiamo dire che le soluzioni della disequazione saranno:

 

4.          

Applicando la formula risolutiva si calcolano le eventuali radici dell’equazione associata:

 

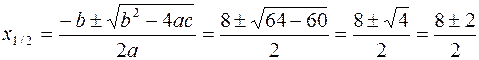
Quindi possiamo scrivere

Studiando il segno del prodotto otteniamo:

:                             :    

Quindi si ha:

                                                                                                 

                                                                                                   valori di x

                _ _ _ _ _                                                       

               _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

 

Segno del          +                  _                        +

Prodotto

 

le soluzioni della disequazione saranno:

 

5.          

Applicando la formula risolutiva si calcolano le eventuali radici dell’ equazione associata:

 

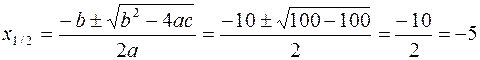
Quindi possiamo scrivere:      e la soluzione della disequazione sarà: .

 

Osservazione: siccome la disequazione chiede le soluzioni “”, la soluzione della disequazione sarà solo  “”, se al contrario ci fosse stato solo “< 0” allora la disequazione sarebbe stata impossibile, cioè senza soluzioni.

 

6.              

 

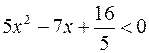
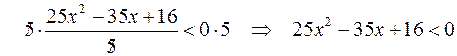
Applicando la formula risolutiva si calcolano le eventuali radici dell’ equazione associata:

 

 

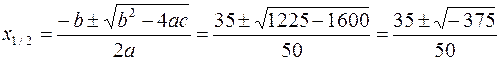
Poiché – 375 è negativo, la sua radice quadrata non esiste quindi, la

disequazione è impossibile, cioè non ha soluzioni.

 

 

 

 

Video - esercizi risolti…   

Torna alla Home Page