ESEMPI SVOLTI DISEQUAZIONI DI 1° GRADO INTERE
1)
dividiamo entrambi i
membri per 6 e otteniamo 
semplificando si
ottiene 
.
Ciò vuol dire che tutti i numeri più grandi di 
sono
soluzioni della disequazione.
2)
, poiché il
coefficiente della x è negativo, bisogna dividere entrambi i membri per – 6 e cambiare
il verso della disuguaglianza 
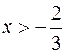
Quindi
tutti i numeri più grandi di 
sono soluzioni della
disequazione.
3)
è una disuguaglianza verificata per qualunque valore
di x, quindi l’insieme delle soluzioni coincide con l’ insieme R dei
numeri reali.
4) 
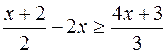
il minimo comune multiplo tra i denominatori e' 6, quindi si ottiene
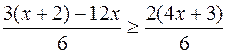
Eliminiamo i
denominatori ed eseguiamo le operazioni ai numeratori
Dividiamo
entrambi i membri per – 17 e cambiamo il verso della disuguaglianza otteniamo 
.
Eseguiamo prima di
tutto i calcoli algebrici 
e semplificando avremo
.
Una cosa
molto utile!
Vediamo ora un modo molto utile per rappresentare con un grafico le soluzioni di una disequazione.
Consideriamo ad esempio le soluzioni dell’ ultimo esercizio:
Abbiamo detto cosa vuol dire: tutti i numeri più piccoli di – 1 sono soluzione della disequazione.
Tracciamo la retta orientata sulla quale rappresentiamo i numeri, che genericamente indichiamo con x e vi posizioniamo il valore trovato – 1. Sulla retta l’ ordinamento dei numeri è quello naturale crescente da sinistra verso destra.
- 1 x
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Usiamo le seguenti convenzioni:
· La linea continua rappresenta la zona in cui la disequazione è verificata, cioè la zona in cui si trovano i numeri minori di – 1
· La linea tratteggiata rappresenta la zona in cui la disequazione non è verificata, cioè la zona in cui si trovano i numeri più grandi di – 1
Altri esercizi risolti
Torna alla Home Page