EQUAZIONE DI UNA RETTA e SUO GRAFICO NEL PIANO CARTESIANO.
Prima di tutto dobbiamo dare una definizione generale, quella di
funzione reale di una variabile reale
Date due grandezze variabili x e y , si dice funzione reale di una variabile reale e si scrive y = f(x), una relazione o legge che associa ad ogni valore reale di x, uno e un solo valore reale di y.
x viene chiamata variabile indipendente,
y viene detta variabile dipendente, perché dipende dai valori assegnati alla variabile x.
Per ogni funzione si parla di:
DOMINIO = insieme dei valori reali che possono essere attribuiti alla variabile x,
e di
CODOMINIO = insieme dei valori reali assunti dalla variabile y.
Esempi di funzioni numeriche, cioè di funzioni che hanno come dominio e codominio insiemi numerici possono essere:
oppure 
oppure 
.
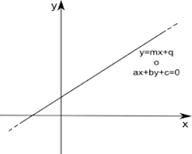
La retta è una funzione lineare, cioè una funzione espressa da una equazione di 1° grado nelle variabili x e y.
L’ equazione di una retta si può trovare scritta in due forme:
a)
forma implicita o normale : 
dove a, b, c
sono numeri reali.
b) forma esplicita : y = mx + q
L’ equazione in forma esplicita si ricava da quella in forma implicita e viceversa:
esplicitando l’ equazione rispetto alla variabile y, per esempio si passa dall’ equazione in forma implicita a quella in forma esplicita:
dividendo entrambi i membri
per 
si
ottiene 
.
Di
solito si indicano 
e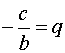 
per cui troviamo l’ equazione in
forma esplicita y = mx + q .
m è detto coefficiente angolare della retta , mentre q è detto termine noto.
ESEMPIO di passaggio dall’ equazione in forma implicita a quella in forma esplicita.
Data
la retta di equazione 
trasformarla in forma esplicita.
Bisogna ‘isolare’ la variabile y al primo membro dell’ equazione, cioè, applicando le proprietà delle equazioni, fare in modo che rimanga appunto ‘da sola’ al primo membro dell’ equazione, con coefficiente numerico uguale a 1. Quindi scriveremo:
e dividendo entrambi
i membri per 4 : 
;
si possono anche scrivere i denominatori separati : 
Come sappiamo le rette nel piano sono infinite; alcune hanno posizioni privilegiate rispetto al sistema di riferimento cartesiano e per questo le equazioni che le rappresentano sono particolari, in qualche modo più semplici.
EQUAZIONI DI RETTE PARTICOLARI
Nel piano cartesiano ortogonale ad ogni funzione y = f(x) si può associare un grafico, cioè un disegno, che si ottiene unendo tutti i punti P(x; y), le cui coordinate cartesiane, sostituite nella funzione, la verificano.
Per
esempio il punto A(1; 2) appartiene al grafico della retta 
in quanto se sostituiamo alla x
il valore 1 e alla y il valore 2 otteniamo 2 = 1 + 1, cioè 2 = 2, che è una
uguaglianza verificata.
Ma come si
fa per tracciare il grafico di una retta data l’ equazione che la rappresenta?
Esercizi su Retta
Equazione della retta passante per due punti A e B
A(1;3) e B(2;4)
A(-2;7) e B(1;1)
A(0;9) e B(-3;0)
A(-2;-4) e B(1;-1)
Intersezione tra una retta e gli assi cartesiani
Tutte le videolezioni su retta nel Piano Cartesiano
Torna alla Home Page