Scomposizione di un polinomio mediante la regola di Ruffini.
Possiamo scomporre un polinomio in fattori mediante la regola di Ruffini (che in questo discorso diamo per nota), procedendo nel modo seguente:
1. Troviamo tutti i divisori (p) del termine noto;
2. Troviamo tutti i divisori (q) del coefficiente del termine di grado massimo
3. Calcoliamo i valori del polinomio sostituendo alla x i valori p/q
4. Eseguiamo la regola di Ruffini con il valore p/q che annulla il polimonio.
MA
CHE VUOL DIRE
Con alcuni esempi capiremo meglio… 
1) 2x3 - 5x2 + x + 2
Consideriamo i divisori (p) del termine noto 2 cioè +1, -1, +2, -2 .
Consideriamo tutti i divisori (q) del coefficiente del termine di grado massimo rispetto a x in questo caso di x3 ossia 2 e cioè +1, -1, +2, -2.
Prendiamo
tutte le frazioni del tipo p/q: +1, -1, +2, -2, +1/2, -1/2 e vediamo quali di
queste frazioni sostituite alla x annullano l’ equazione.![]()
Sostituendo -1 al posto della x si ha 2(-1)3-5(-1)2+(-1)+2 = -2-5-1+2 ≠ 0
Sostituendo 1 al posto della x si ha 2(1)3-5(1)2+1+2 = 2-5+1+2 = 0
Quindi si applica la regola di Ruffini con il valore 1 e si ha il seguente quadro:
|
|
2 |
-5 |
1 |
2 |
|
1 |
|
2 |
-3 |
-2 |
|
|
2 |
-3 |
-2 |
0 |
Quindi il polinomio 2x3-5x2+x+2 si scompone in (x-1)(2x2-3x-2);
rimane da scomporre ancora il trinomio 2x2-3x-2.
Possiamo usare di nuovo la regola di Ruffini:
consideriamo i divisori (p) del termine noto 2 cioè +1,-1. +2,-2
consideriamo tutti i divisori (q) del coefficiente di x2 ossia 2 cioè +1, -1, +2, -2.
Prendiamo tutte le frazioni del tipo p/q: +1,-1,+2,-2,+1/2, -1/2
Il polinomio 2x2-3x-2 si annulla per x = 2, infatti si ha: 2(2)2-3(2)-2=8-6-2 = 0
Possiamo continuare il quadro precedente con il valore 2 e otteniamo:
|
|
2 |
-5 |
1 |
2 |
|
1 |
|
2 |
-3 |
-2 |
|
|
2 |
-3 |
-2 |
0 |
|
2 |
|
4 |
2 |
|
|
|
2 |
1 |
0 |
|
2x2-3x-2 = (x-2)(2x+1)
Quindi la scomposizione del polinomio iniziale è:
2x3- 5x2+x+2 = (x-1)(2x2-3x-2) = (x-1)(x-2)(2x+1)
2) x3 – x - 6
Gli eventuali valori che annullano il polinomio sono da ricercare tra tutti i divisori del termine noto poiché il coefficiente di x3 è 1 e cioè tra i numeri +1; -1; +2; -2; +3; -3; +6; -6.
P(1) = 13-1-6 = 1-1-6 = -6 ≠ 0
P(1) = 13-1-6=1-1-6 = -6 ≠ 0
P(-1) = (-1)3-(-1)-6 = -1+1-6 = -6 ≠ 0
P(-2) = (-2)3-(-2)-6 = -8+2-6 = -12 ≠ 0
P(2) = (2)3-2-6 = 0
P(3) = (3)3-3-6 = 27-3-6 = 18 ≠ 0
P(-3) = (-3)3+3-6 = -30 ≠ 0
P(6) = (6)3-6-6=204 ≠ 0
P(-6) = -216 ≠ 0
L’ unico valore che annulla il polinomio è 2 quindi facciamo il quadro di Ruffini con 2
![]()
![]() 1 0 - 1 -6
1 0 - 1 -6
![]() 2
2 4 6
2
2 4 6
1 2 3 0
Alla fine il polinomio si scompone in x3-x-6=(x-2)(x2+2x+3).

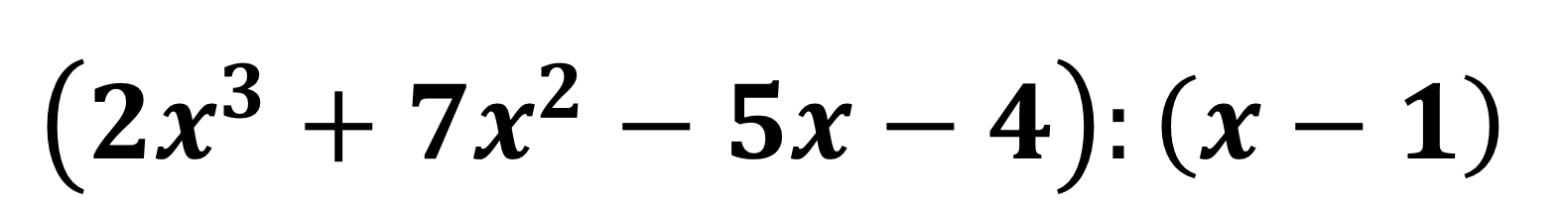 .
.

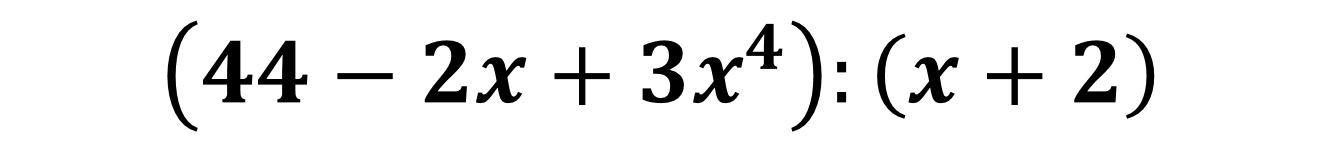 .
.

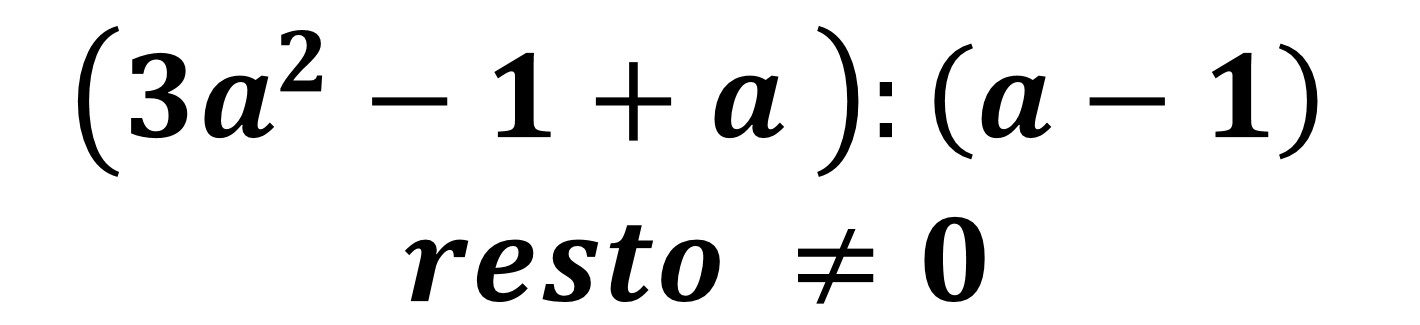
 Torna alla Home Page
Torna alla Home Page