Equazioni di 1° grado frazionarie
Un’ equazione si dice frazionaria quando l’ incognita compare al denominatore di almeno una delle frazioni presenti.
Esempi:
1)  non è un’ equazione
frazionaria perché al denominatore ci sono soltanto numeri.
non è un’ equazione
frazionaria perché al denominatore ci sono soltanto numeri.
2)  è invece un’ equazione
frazionaria, in quanto al denominatore è presente l’ incognita ( x ).
è invece un’ equazione
frazionaria, in quanto al denominatore è presente l’ incognita ( x ).
Come si risolve un’ equazione frazionaria?
Cerchiamo di capirlo con un’ esempio svolto e risolviamo quindi la seguente equazione frazionaria:
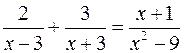
Per risolvere l’ equazione bisogna prima di tutto escludere i casi particolari in cui le frazioni algebriche presenti perdono di significato, cioè i casi in cui i denominatori delle stesse si annullano.
Nel nostro caso deve essere: ![]() ,
, ![]() . Poiché
. Poiché ![]() ritroviamo
gli stessi valori e quindi non dobbiamo discutere altre situazioni.
ritroviamo
gli stessi valori e quindi non dobbiamo discutere altre situazioni.
Se tra le soluzioni trovassimo x = 3 oppure x = - 3 dovremmo escluderle in quanto non accettabili.
Ora possiamo cominciare… portiamo prima tutti
i termini a sinistra dell’ uguale, rispettando le proprietà delle
equazioni… osserva
osserva
il testo e il passaggio successivo (entrambi in giallo): la frazione che abbiamo spostato dal 2° al 1° membro ha davanti il segno -. Ricordi la proprietà delle equazioni il cui effetto è che tutto quello che sposti da un membro all’ altro cambia di segno? Accade in tutti i tipi di equazioni e nel nostro caso il 1° membro dell’ equazione è diventato un’ espressione con le frazioni algebriche:
 Bisogna allora
ricordare tutti i procedimenti
Bisogna allora
ricordare tutti i procedimenti
imparati per eseguire le addizioni e le sottrazioni di frazioni algebriche
Il m.c.m. tra tutti i denominatori è ![]() , quindi
otteniamo
, quindi
otteniamo

Moltiplicando entrambi i membri dell’
equazione per il m.c.m. ![]() si ottiene
si ottiene
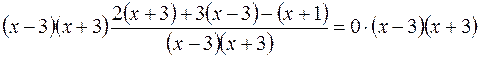
da cui, dopo aver semplificato, segue
che ![]()
 Siamo di fronte ad un’
equazione intera!
Siamo di fronte ad un’
equazione intera!
Risolvendo:
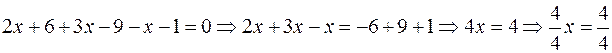
Cioè ![]() . La
soluzione è accettabile, in quanto 1 è diverso da + 3 e da – 3.
. La
soluzione è accettabile, in quanto 1 è diverso da + 3 e da – 3.

· Esaminiamo le condizioni di esistenza delle frazioni algebriche coinvolte
· Portiamo tutti i termini dell’ equazione al 1° membro, rispettando le proprietà delle equazioni
· Svolgiamo le operazioni con le frazioni algebriche presenti ricavando il valore dell’ incognita
· Confrontiamo il valore trovato con quelli eventualmente esclusi nella discussione delle condizioni di esistenza concludendo sull’ accettabilità o meno della soluzione trovata
Videolezioni su Equazioni Fratte
ESERCIZI SULLE EQUAZIONI DI 1° GRADO FRAZIONARIE
 Torna alla Home Page
Torna alla Home Page