Definizione di logaritmo di un numero reale positivo
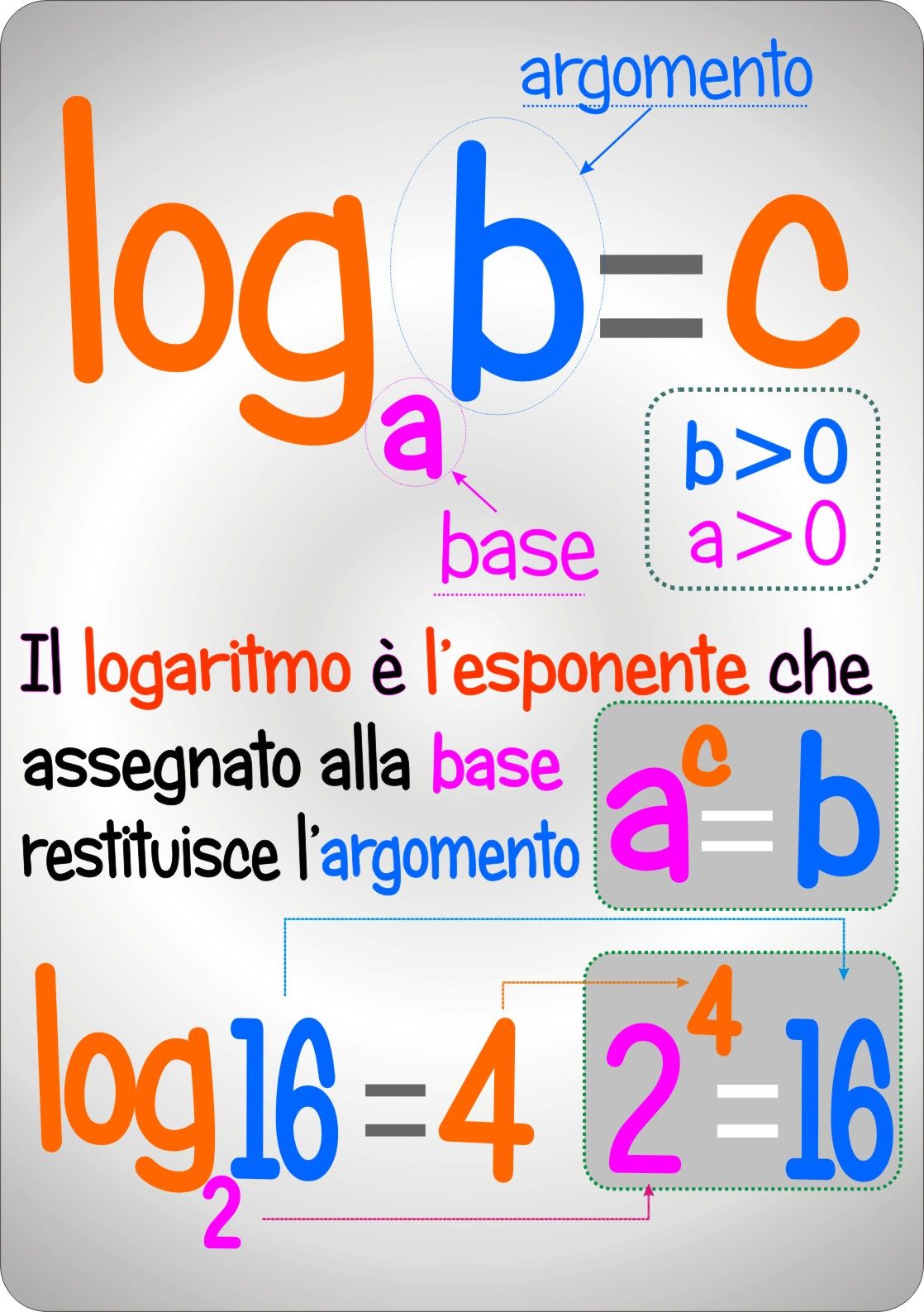
Il logaritmo di un numero b (positivo), in una data base a (positiva e diversa da 1), è l’ esponente x che bisogna dare alla base per ottenere il numero dato, cioè:
Esempi
Il logaritmo di 8 in base 2 (si scrive: 
) è
uguale a 3, perché 3 è l’esponente da dare a 2 per ottenere 8 :
infatti: 
Analogamente:
infatti: 
infatti: 
Quando la base del logaritmo non è specificata questa si assume uguale a 10 (logaritmi decimali o di Briggs) oppure uguale a “e” ( e = 2,7182… , è il numero di Nepero; i logaritmi in tale base e si dicono naturali o neperiani).
I logaritmi in base 10 si dicono anche logaritmi di Briggs per ricordare il matematico inglese Henry Briggs (1561-1631), il quale è noto in matematica per le sue ricerche sui calcoli con i logaritmi e per la realizzazione delle prime tavole dei logaritmi in base 10.
A cosa servono i logaritmi: Schooltoon e Liceo Massimo D'Azeglio (Torino)
Esercizi svolti sui logaritmi: Schooltoon e Liceo Massimo D'Azeglio (Torino)
Lgaritmo : definizione e calcolo
Proprietà dei logaritmi
L’ introduzione delle calcolatrici ha tolto importanza ai logaritmi come strumento di calcolo, ma le funzioni logaritmiche e la nozione di logaritmo hanno assunto un ruolo importante in matematica e trovano numerose applicazioni non solo nell’ ambito matematico o fisico ma anche in campi molto diversi tra loro come quello economico, chimico, biologico, geologico, archeologico…in generale dove bisogna trattare con grandezze che presentano ampie variazioni su un intervallo di diversi ordini di grandezza.
Proviamo a capire con un esempio:
se una grandezza ha variabilità da 1 a 
(1000 miliardi) il
logaritmo decimale di questa grandezza varia solamente da 1 e 12- ciò rende
possibile la rappresentazione grafica di tale grandezza: basta mettere nel
grafico, invece della grandezza stessa, il suo logaritmo decimale. Cioè si usa
una SCALA LOGARITMICA.
Poco dopo la scoperta dei logaritmi fu costruito uno strumento chiamato ‘regolo calcolatore’ composto da due righelli graduati scorrevoli l’ uno accanto all’ altro in cui le tacche sulle scale graduate sono basate sui logaritmi, che permetteva di calcolare moltiplicazioni e divisioni in modo molto semplice.
Il regolo fu via via perfezionato e fino alla diffusione delle macchine calcolatrici divenne l’ inseparabile strumento di calcolo di geometri, architetti ed ingegneri.
Se siete curiosi potete approfondire in autonomia….
Videolezioni sui Logaritmi (definizione, proprietà , equazioni e disequazioni)
Torna alla Home Page